N [rxa cos2
2n mAvAMAa cos
2n mA(QvAa2 cos cp + uAvAa cos (p)a cos cp dX
是绝对角动量在大气中的经向输运,它等于行星动量(右边第一项)和相对动量(第二项)的经向输运之和;(pAE - pAW)为第i山岭东西坡的压差;对所有穿越有关纬度带的山脉和地球表面的其他不规则地形进行了汇总;Xx为下垫面切向风应力的纬向分量;其余的名称是相同的。
式(2.6.3)描述了单位经向延伸的带内角动量的收支情况。为了估计预算的组成部分,我们使用年平均纬向的观测数据风速(图2.16)。它在经向上分布的显著特征
-
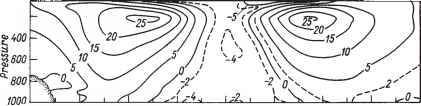
- 图2.16 Peixoto and Oort(1984)风速纬向分量的年平均纬度-高度分布(m/ S)
平面是每个半球环流的三单元结构,在热带和极地纬度有两个正单元,在温带纬度有一个反向单元。可以回忆起,环流的直接环流单元是暖空气上涌和冷空气下涌的环流单元。另一方面,在相反的空气单元中,冷空气上涌,暖空气下涌。低纬度环流的直接环流单元通常被称为环流单元哈得来环流圈,反向单元格为套圈细胞.
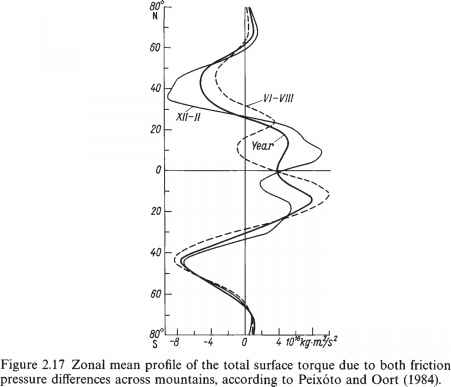
由图2.16可以看出,风速低时的纬向分量大气的水平是向西的(偏东信风)分布在低纬度地区,而在东面(西风)在温带地区。相应地,在第一种情况下,面向风的表面摩擦应力为正,在第二种情况下为负。由此可以得出结论,大气在低纬度向地球传递动量,而在温带从地球获得动量。但是,由于根据牛顿第三定律,地球对大气产生了等量相反(方向上)的作用,人们可以认为,在低纬度地区,它是大气动量的来源,而在高纬度地区,它是动量的汇聚。相对角动量也是如此。为了证实这一点,我们参考图2.17,其中显示了由压力和摩擦力引起的总表面扭矩的子午分布的计算结果。如果这个扭矩倾向于增加大气向东的角动量,也就是说,在式(2.6.3)的最后一项中,切向风应力被相等但方向相反的下垫面的切向应力所取代,这个扭矩就被认为是正的。从图2.16可以看出,相对角动量在热带地区由下垫面向大气的输送,在温带地区由大气向下垫面的输送,其输送方向可能全年不变。
我们注意到大气相对角动量的另外两个来源:环流的北极和南极单元的定位区域。纬度圆的适当半径(臂a cos q>)很小,这就是为什么从下垫面传递到大气的相对角动量也很小。
在热带地区,相对角动量是从下垫面转移到大气的。它随后的命运是这样的:首先,它被哈德利环流的上升分支带到对流层上层,然后它被短暂的涡流输送到中纬度地区,在这里它减少了,以弥补在大气中的损失
大气行星边界层中由于摩擦而产生的相对角动量。
众所周知,固体旋转的速度Qa等于464米/秒,远远大于相对风速u。因此,人们可能会认为,绝对角动量的子午线输运主要是由行星动量输运决定的。但在稳态状态下,绝对角动量的积分(在大气质量上)子午输运不依赖于行星动量输运,因为根据质量守恒定律,风速的积分纬向分量完全等于零。换句话说,绝对角动量的积分经向输运完全由相对角动量输运决定,而相对角动量输运又完全取决于风速的纬向分量和经向分量之间的相关性[wAtfA]。但是,由于绝对角动量在温带地区的无限积累,以及在低纬度地区的无限减去,不会发生,绝对角动量的反向(补偿)传输必须存在。人们很自然地认为这种运输集中在海洋中。让我们来检验一下这种可能性。
首先我们写下预算方程在单位经向延伸的海洋带中求绝对角动量。类比式(2.6.3)可得
2na cos q> - [m0M0]——MMT0 = -
Dt a DTP
+ 2n[zx]a2 cos2 cp, (2.6.4)
在哪里
* 2记
MMTn = m0v0M0a cos (p dA o o -
是海洋中绝对角动量的经向输送;(Poe - Pow)是中部大陆东西边缘的压力差海洋山脊以及其他穿越带状带的底部波动;假定海底的切向应力与自由海洋表面的切向应力相比可以忽略不计。
我们比较了大气和Jhe^海洋中绝对角动量经向输运的估计。让我们假设相关项[«a^a!大气和海洋单位柱的质量(mA和mQ),以及大气和海洋在纬向上的延伸,分别等于104,3 x 10"3和2。那么0(MMTJMMTo)«102,即海洋中绝对角动量的经向输运仅为大气中绝对角动量的1%,因此不能补偿大气中纬度绝对角动量的积累。
考虑到这一点,将年平均条件的式(2.6.4)改写为
X (Poe - Pow)a cos
这表明海洋表面摩擦力的扭矩被压力差(平均值之差)所产生的扭矩所平衡海洋的水平),因此,与大气不同,海洋绝对角动量的重分布是在纬向,而非经向(图2.17)。
因此,我们只有一种可能:通过绝对角动量在地球固体中的经向运动来闭合绝对角动量的循环。这与奥尔特(1985)的观点一致,他提出了描述
温和的
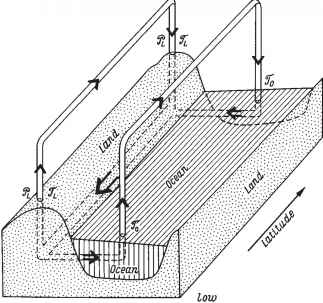
图2.18 Oort(1985)提出的海洋-大气-岩石圈系统绝对角动量循环示意图。压力和摩擦力矩分别用符号0>、3~表示;指数L表示属于陆地,指数O表示属于海洋。
温和的
图2.18 Oort(1985)提出的海洋-大气-岩石圈系统绝对角动量循环示意图。压力和摩擦力矩分别用符号0>、3~表示;指数L表示属于陆地,指数O表示属于海洋。
绝对角动量的周期。这张图的清晰几乎掩盖了它的缺点,这与解释地球固体中绝对角动量传输机制的困难有关。
2.7碳预算
碳在其他化学元素中的独特地位首先是由这样一个事实决定的:碳原子由于其电中性,很容易彼此相互作用,也很容易与其他元素的原子相互作用,产生稳定的有机化合物,从而对地球上的生物过程和生命进化产生关键影响。此外,碳被包含在像二氧化碳这样的重要化合物的组成中,二氧化碳在形成地球辐射中的作用是很难高估的。
碳含量。大气中的碳主要以两种稳定化合物(二氧化碳co2和甲烷CH4)和一种不稳定化合物(一氧化碳CO)的形式存在,这种化合物很快被氧化成二氧化碳。
1988年1月,第一个化合物的体积浓度为351 ppm,第二个化合物的体积浓度约为1.6 ppm,第三个化合物的体积浓度约为0.1 ppm。很明显,大气中的碳含量几乎完全由二氧化碳决定。
对大气中二氧化碳浓度的定期精确测量开始于国际地球物理年(1957-1958)在莫纳罗亚(夏威夷)。在1960年至1963年期间,南极站(南极洲)开始运作,今天有30多个站用于二氧化碳的背景监测,这些站都远离工业中心。对这些气象站数据的分析表明,大气中二氧化碳浓度具有明显的季节性变化相移在陆地生态系统中有机物物质的形成(生产)和分解(破坏)过程中。季节变化的最大幅度(~ 8.2 ppm)已在位于北美北方森林地区的黄金湾(阿拉斯加)和欧亚大陆被记录下来。最大振幅向北减小到约3 ppm在莫纳罗亚和南半球的0.5-1.5 ppm,在那里,有机物质的生产和破坏之间的相位转移主要集中在美洲的森林中热带带很低。
大气中co2体积浓度的大尺度空间变化小于局地季节变化。因此,分别位于3397米和3米高度的莫纳罗亚(Mauna Loa)和库穆塔希(Kumutahi)两个相邻台站8年(1976年至1983年)的体积浓度平均值彼此之间仅相差0.4±0.3 ppm,而位于地球北极和南极地区的台站同期的平均值相差3.2 ppm。大气中co2体积浓度的这种相对较小的空间变异性是由大气的快速混合(与更新时间相比,见下文)所解释的,其特征时间尺度(如表1.1所示)不超过106秒。
单位大气柱中的碳含量由表达式CA = (PclVcoJm^M确定,其中CA = i0~6(pCO2/p)qCO2为co2的比浓度;qCOl = 106 x Pco2/ps为co2的体积浓度;pCOl和ps分别为二氧化碳分压和海平面大气压;mA为单位横截面大气柱的质量;pc、pC02、p分别为碳、二氧化碳、空气的分子量;符号A表示对质量求平均的运算。根据这个表达式,1988年1月大气中的碳含量为745千兆吨(1千兆吨= 109吨)。作为比较,在工业革命之前,即在1860年之前,它等于594千兆吨。
用C02 S C02 (diss)和C02 (diss) + H20 S H2C03两个表达式来描述co2在水中的溶解,定义了碳酸H2C03的水化现象和化学平衡条件。溶解需要几分钟,由平衡常数K0 = [H2C03]/[C02]决定,其中[C02]和[H2C03]是溶解的二氧化碳和溶解的碳酸的浓度。如果海洋中的无机碳含量仅由这一过程控制,那么它将达到其现值的1%。实际上,二氧化碳不像氧气、氮气或氩气等惰性气体那样是惰性气体,这就是为什么二氧化碳在水中溶解时,会与地壳的物质发生反应,并形成其他化合物,这些化合物逐渐积聚在海洋中,结果它们的浓度比碳酸的浓度大许多倍。
海洋中主要的碳化合物是碳酸氢盐离子HC03。其含量占海洋无机碳总量的百分比约为95%。碳酸氢盐离子是由失去质子的碳酸解离形成的。该阶段立即进行,用化学平衡条件H2C03 S HCOf + H+描述,解离常数= [HC03][H+]/[H2C03],其中[HC03]和[H+]是碳酸氢盐和氢离子的浓度。
下一阶段是碳酸氢根离子的解离和形成碳酸盐离子CO\~。化学平衡的合适条件为hc03sc03 ~ + H+,由解离常数K2 = [C0§"][H+]/[HC03]决定,其中[C03~]为碳酸盐离子的浓度。碳酸盐离子是溶解的二氧化碳与碱反应的最终产物。它在海洋中的浓度不断增加,直到达到碳酸钙CaC03的溶解度极限。CaC03的溶解用CaC03 S Ca2+ + CO2-表达来描述,解离常数Ks由钙离子[Ca2+]和碳酸盐离子[C03~]与方解石和文石两种晶体形式中的一种平衡共存的钙离子浓度的乘积决定。
我们定义海洋中无机碳的总浓度cQ为cQ = [C02] - i - [HCO3] + [CO2-]。气相色谱法获得的现有数据表明(见高桥等人,1981年),海洋表面无机碳的总浓度从1900 ^imol/kg开始随纬度增加赤道区在北纬55°,最高可达2150 ^mol/kg;在北纬55-60°,最高可达2250 (imol/kg)。它也随着深度的增加而增加,但只是在海洋上层两公里的范围内。表层无机碳总浓度的下降是由浮游植物光合作用过程中无机碳的消耗和与大气的co2交换在一定程度上造成的,而1000米以下总浓度的增加是由浮游植物和浮游动物下落残渣的分解和软质有机物的氧化引起的。根据Kobak(1988)的研究,海洋中无机碳的总含量为38 200 GtC。其中的864千兆吨碳当量,略高于大气中的含量,是在海洋100米的上层。
过去几年从卫星图像、航空摄影和地面研究中获得的数据使我们能够确定(见Kobak, 1988)陆地生物群中有机碳的总含量不超过560千兆吨碳当量这一事实。请注意,20年前估计为827千兆吨碳当量。造成这些差异的原因是关于森林生态系统中具体碳含量(指单位面积)及其所占区域的初始信息有限和不准确。
目前,地球上生命物种的多样性是由其陆地居民决定的:被子植物和昆虫。最后提到的类群有100万个物种。在海洋中,动植物的具体种类要少得多(约有30000种植物和160,000种动物),这是由控制物种组成和生物群密度的生态和气候条件的变异性较低(比在陆地上)所解释的。海藻是海洋中有机物的主要生产者。已知的水生植物约有3万至3.5万种,其中一半以上生活在海洋中。
海洋中有机碳的主要成分是溶解性有机物(DOM),是介于生物和生物之间的中间物质无机物,结合有机碳的真溶液和胶体以及大小从0.45到1 |im的颗粒。根据实验数据,海洋中DOM的平均浓度为1.36 + 0.20 mg/1,相当于整个海洋体积的1800-2000 GtC。
海洋中有机碳的另一种存在形式是悬浮有机质(SOM),包括浮游植物和浮游动物的活细胞、生物体的残留物、骨架形成的有机质、陆源和风成流入,以及从溶液中沉淀、吸附和聚集的粒径大于1pm的有机物。SOM在海洋中的浓度远低于DOM,平均为53 + 26(¿m/1)。它的最大值落在高产地区,最小值落在低产地区和深海层。海洋中SOM总含量估计为25.5 + 1.5 GtC。
其中约50%是在1000米以上的深度,那里的细菌活性很低,有机物的氧化非常缓慢。约等量的SOM (15-20 GtC)未矿化,逐渐下沉到海底。
最后,海洋中碳的第三种存在形式是有生命的有机物。目前对植物和动物质量的所有估计都接近3亿吨碳当量。因此,DOM、SOM和活有机物的总含量的估价值为100:1.4:0.15。这种“质量金字塔”是由海洋中有机物的生产和破坏平衡造成的。换句话说,它反映了不同形式的有机物的不同稳定性(从分解的角度来看)。
生物(主要是植物和光合作用生物)在重要功能过程中产生的有机物参与了快速的生物转化,也积累在相对稳定(在破坏意义上)的复合体中,形成陆地上的土壤有机物和海洋中的水腐殖质。在生化和化学过程的作用下,有机残留物受到破坏,部分有机质转化为矿物化合物(二氧化碳、氨、亚硝酸盐和硝酸盐等);剩余部分转化为更稳定(缓慢氧化)的有机形式。这就是为什么,例如,习惯上将土地上的所有有机残留物分为三类:蔬菜落叶和有机衬底(落叶、树木、灌木和草覆盖的死亡部分);不稳定生化化合物(未完全修饰的蔬菜残渣、代谢产物和新形成的腐殖质);稳定的生化化合物(腐殖质、泥炭、腐泥等),含量分别为84.2、673和1346 GtC。因此,土壤中有机碳的总含量为2104 GtC,与海洋中溶解有机质中的有机碳含量基本一致。
土壤碳含量最多的是北方带,最少的是极地带,分别占总含量的35.1%和6.5%。然而,请注意,极带有机碳的最低含量并不是由其浓度低(甚至高于热带、亚热带和亚北纬带)来解释的,而是由极带面积小来解释的。
海洋中的有机物也分为稳定和不稳定两类,其中大部分是自生的(由活生物体形成)。不稳定分数的垂直变异性大于稳定分数。可以这样说,海洋表层腐殖质水的浓度等于~2.2 × 10”3gC/l,在3000米的尺度上等于~1.5 × 10~3gC/l,而不稳定部分的浓度,仅由浮游动物和细菌的生命功能过程决定,在海洋厚度的范围内可以相差100倍。
对海洋和大陆沉积物中碳含量的估计是相当接近的。最近的估计(见Budykoet al., 1985)证实地球沉积层含97.8 × 106 GtC,其中碳酸盐86 × 106 Gt,有机碳11.8 × 106 Gt。
碳源和碳汇.我们已经说过,大气中的碳含量与陆地生物群的重要功能过程密切相关,而二氧化碳实际上是碳的唯一来源(至少目前是)。20世纪20年代初,首次获得了证实大气中二氧化碳含量与植物同化活性之间存在关系的实验数据。20世纪50年代光声气体分析仪的出现和测量精度的提高,为研究植物群落中二氧化碳同化的物理机制和创建光合作用的定量理论提供了可能性。
大气和蔬菜群落之间的碳交换强度以纯初级生产为特征,其定义为自养生物和异养生物的总初级生产(有机物形成的速率)和呼吸损失(呼吸作用下有机物破坏的速率)之间的差异。自养生物是吸收植物碳的生物无机化合物,异养生物是利用有机物的生物。如果总数初级生产是生态系统是大气的碳汇,比呼吸作用的损失要高;否则它代表了大气中的碳源。根据Kobak(1988)的数据,所有森林、草原和苔原蔬菜群落的初级生产总量等于118.2千亿吨碳当量/年。
让我们将自养生物呼吸的损失定义为初级生产总量与碳光合同化速率之间的差值,而异养生物呼吸的损失定义为上层土壤有机质矿化速率与有机质转化为腐殖质的速率之和。根据Kobak(1988),碳的光合同化速率为58.2 GtC/年,而有机质矿化及其转化为腐殖质的速率为41.4和2.5 GtC/年。有机质向腐殖质转化的速率由两个组成部分组成,表征土壤腐殖质不稳定组分(1.44 GtC/年)和稳定组分(1.04 GtC/年)的形成速率。利用这些估计和上面提到的估计,我们发现陆地生物群的纯初级生产(等于光合作用同化率减去有机质矿化率)及其转化为腐殖质的总量必须达到58.2 - 41.4 - 2.5 = 14.3 GtC/年。因此,陆地生物群充当了大气的碳汇。
二氧化碳进入大气的通量不仅来自陆地植被的呼吸作用,还来自所谓的土壤呼吸(土壤排放二氧化碳),这是微生物氧化土壤有机物和植被根系呼吸作用的结果。但由于在没有其他碳源和碳汇的情况下,其通过光合作用从大气中撤出的量只能通过土壤呼吸来平衡,因此必须与碳的光合同化量相等,即58.2 GtC/年。该值的部分(41.4 + 2.5 = 43.9 GtC/年)由矿化有机质和腐殖质的破坏决定;另一部分是由植物根系的呼吸作用决定的。
与陆地植物群落相反,在海洋生态系统中,碳并不是限制光合作用的因素。其中一个因素是短波太阳辐射强度,当光合作用停止时,短波太阳辐射强度不小于2.08 W/m2的极限值。适合这个值的深度称为光补偿深度。在这个深度以上,光合作用同化的强度大于呼吸作用的损失,而在这个深度以下则相反,浮游植物只能由于先前形成的有机物而生存,也就是说,由于转化为异养营养物。
限制光合作用的另一个因素是海水中存在的生物元素——硝酸盐NO3和磷酸盐HPO4”。的确,根据雷德菲尔公式
106C02 + I6NO3 + HPOr + 18H+ + 122H20 S
(CH20) j06 (NH3)!6(h3 P04) + 13802,描述了光合作用的过程及其对有机物的反破坏过程,每消耗106摩尔的二氧化碳进行光合作用,消耗16摩尔的硝酸盐和1摩尔的磷酸盐。由此可见,浮游植物细胞中碳、氮、磷含量的比例为106:16:1,氮、磷的缺乏限制了碳同化的强度。
如果我们把浮游植物的异养营养归为二次生产,把同样的归为化学合成,它使用化学反应的能量作为来源,那么光合作用对碳的同化将代表海洋生物群的纯粹初级生产。它的许多估计主要是用放射性碳方法得到的。其中最可靠的是在23-46 GtC/年的范围内。研究还表明,75%的纯初级生产发生在公海,17.5%发生在大陆架,4%发生在河口,只有0.5%发生在局地上升流区.关于海洋生物群产量的季节变化的信息可以归为非常近似的。我们所知道的一切都可以归结为:在低纬度浮游植物生产全年大部分时间不变化,但在温带地区,它经历明显的季节变化,春季增加,夏季减少。夏季的减少与浮游植物被食草性浮游动物捕食有关,特别是与生物元素的缺乏有关,这些生物元素从深层涌入,被上层混合层底部的突然温跃层阻挡。秋季,垂直混合增强季节性温跃层退化后,浮游植物产量再次增加。在高纬度地区,只有一个(夏季)产量峰值被记录下来。这些陈述得到卫星对海洋表面进行彩色扫描的数据的支持,这些数据可以恢复水中的叶绿素浓度。
除了海洋中有机质形成的自吞机制(光合作用)外,还有另一种机制——异吞机制,其特征是有机物随着河流和地下径流流入,以及含有有机碳的悬浮颗粒和风积物从陆地上去除。根据Kobak(1988)的说法,海洋中这种有机物来源的强度为“1千兆吨碳当量/年”。其中河流径流贡献0.21 GtC/年,地下径流贡献0.06 GtC/年,悬浮颗粒贡献0.4 GtC/年,风沙物质贡献0.3 GtC/年。
植物和动物的终生分泌物以及异养生物(细菌)对植物和动物分泌物和残留物的分解补偿了有机物的自体和异养性流入。由此产生的溶解有机质和悬浮有机质的产量分别为1.08 GtC/年和1.0-3.0 GtC/年(见Kobak, 1988),这意味着2-5%的纯初级产量进入了溶液,大约相同数量的产量被沉淀出来。在生化、化学反应过程中形成的沉淀有机质受到破坏,然后以0.9 ~ 2.9 GtC/年的速度溶解,使沉积沉积物中有机质的积累不超过0.1 GtC/年。
海洋-大气界面的碳交换。如前所述,在所有含碳的大气气体中,只有二氧化碳的浓度足够高。因此,海洋-大气界面的碳交换是由二氧化碳通量决定的。1986年,美国哥伦比亚大学的Lamont Doherty地质观测站在直接测量水和空气中二氧化碳分压差的基础上,首次估算了二氧化碳通量的时空变异性。然后由Ariel et al.(1991)进行了修订。结果发现,海洋赤道区(10°N-10°S)是大气的碳源。在这里,由于强大的上升流保证了向富含碳和生物基因的深水表面的输出,并且由于二氧化碳在水中的溶解度较低(后者是由于温度较高),海洋向大气的碳转移量在大西洋为0.14 GtC/年,在印度洋为0.05 GtC/年,在太平洋为0.54 GtC/年。这些差异是由不同的强度造成的赤道上升流.
在副热带环流在北半球(北纬10°N-40°N)和南半球(北纬10°S-40°S),情况更加多样:在北半球,太平洋和大西洋是大气碳汇,印度洋是碳源。分别为-0.01、-0.19和0.05 GtC/年。在南半球的亚热带环流中,海洋向大气的碳转移发生在大西洋(0.04 GtC/年),大气向海洋的碳转移发生在太平洋(- 0.20 GtC/年)和印度洋(- 0.21 GtC/年)。同样,从海洋向大气的碳转移发生在太平洋北部次极区(0.17 GtC/年),从大气向海洋的碳转移发生在大西洋北部次极区(-0.38 GtC/年)和南部次极区(-1.39 GtC/年)以及南部次极区(-0.83 GtC/年)。
一般而言,如Ariel et al.(1991)所示,海洋吸收大气碳的速率为-2.21 GtC/年。在这里,与以前一样,通量的负值与从大气向海洋的碳转移相一致,而正值则相反。请注意,海洋-大气界面的年平均全球平均碳通量不是零,在没有任何长期扰动的情况下是零。Ariel等人(1991)提出的一些论点支持这种不平衡的人为起源。
碳更新的时间。自然的特征:上文所提到的自然的(不受自然影响的)特征人为影响)碳循环及碳更新次数如表2.4所示。让我们把注意力转向以下三个事实。首先,自然碳循环在大气、海洋和生物圈中是封闭的,但在岩石圈中是不封闭的,因此在地球上气候系统作为一个整体。这是由于忽略了沉积岩和火山岩形成的沉积层与深层地球层之间的相互作用:在这一过程中,有机碳以碳酸盐沉积物的形式在海洋底部积累,即从生物圈到岩石圈的净通量碳必须通过从深层地球层向大气和海洋排放火山二氧化碳来补偿。
其次,根据表2.4的数据,海洋和大陆的大多数古代沉积物和沉积物的年龄,如果按照碳含量与特征的积累或侵蚀速率之比来估计,应该不超过1亿年。换句话说,在整个地球地质历史中,沉积岩一定是不断更新的。
乍一看,这一结果与已知事实相矛盾,特别是与在Ameralik-Fjord(格陵兰岛西部)入口发现的沉积岩相矛盾38亿年年。这种矛盾可以用海洋中沉积堆积速率和大陆上侵蚀速率的可变性来解释,因此也就可以用现在的数值来解释其他地质时期的不可能。在这方面,让我们回顾一下中石炭世和晚石炭世(3.46 - 2.32亿年前)碳酸盐沉积物积累的减少,或者所谓的沉积沉积序列中断(没有沉积物积累的间隔),复发率从始新世时期开始的40-60%变化到始新世时期结束的70-76%(5800 - 3700万年前)。至于大陆侵蚀的速度,可以从代表大陆侵蚀基础的平均海平面的变化来判断。在过去的5.7亿年里,最显著的300-350米的侵蚀增加发生在晚期,同时陆源物质向海洋的输出突然减少白垩纪(1 - 6700万年前)。这次事件和海洋过犯它的起源是什么构造过程导致了非洲大陆和欧亚大陆的汇合以及特提斯海洋的退化。
人们应该记住,对沉积沉积中碳积累速率的估计是相当近似的,最重要的是,海洋中最古老的沉积沉积的年龄是由板块构造决定的,其特征时间尺度为1.5亿年,而在大陆上,它是由持续时间决定的
花岗岩片的存在具有«40亿年的特征时间尺度。因此,表2.4中的数据与在古代地层组成中发现的粉砂沉积物的数据并不矛盾。
应该特别强调的第三种情况是碳循环的不同组成部分的更新时间不同。的确,从表2.4可以看出,碳更新时间为0.1年,海洋生物群的碳更新时间更短;植物落叶和有机底层约1年;大气、陆地生物区系和海洋中悬浮有机物大约十年;数百年,甚至数千年,海洋中的无机碳含量,溶解有机质和土壤腐殖质;最后,海洋和大陆上的沉积物需要数亿年的时间。这种更新时间的多样性是碳循环中三个亚循环分离的基础:流动亚循环,描述了海洋-大气系统中有机质转化和碳循环的过程,时间尺度约为103年及以下;描述海水与碳酸盐沉积物相互作用过程的地球化学亚旋回,时间尺度约为104-105年;地质亚旋回,描述有机质埋藏和变质过程,以及地幔脱气过程,时间尺度约为106年以上。
我们对时间尺度小于103年的过程感兴趣。这一限制相当于固定缓慢(时间尺度超过103年)的碳亚周期特征。在这种情况下,大气-海洋-生物圈-岩石圈系统中碳的预算方程采用如下形式:cA和cQ是大气和海洋中无机碳的特定浓度;cLB(见下文)、cOB和cL是有机碳在陆地和海洋生物群以及岩石圈中的特定浓度;CA = mAcA和CG = m0c0为单位横截面大气柱和海洋柱中的无机碳含量;COB = mQcOB, CLB = mLcLB和CL = mLcL是相同的,但对于海洋和陆地生物群以及岩石圈中的无机碳而言;Q°s为海洋-大气界面的碳通量(气体交换);Q£B和QcB为无机dCJdt + V mAvAcA = -<2°s -Q™,dCJdt + V-i=Q2S-Q2\ dCOB/dt + V mA vACqB = <2c®- Qc,
dChB/dt = Q™- QhB, dCJdt + V-m^L = Qh* Qh,
大气和海洋中的碳源和碳汇以单位面积为单位;<2¿B为陆地生物群的快速组成部分与单位面积归一化的岩石圈之间的碳交换强度;Qq和是岩石圈和海洋中碳循环的快组分和慢组分之间有机碳交换的强度,以类似的方式归一化;所有其他名称都是一样的。
我们将式(2.7.1)对整个地球表面积分,式(2.7.2)和式(2.7.3)对海洋表面积分,式(2.7.4)和式(2.7.5)对陆地表面积分,然后相加。结果我们得到了等式
3 ({C0} / {Ca} + 0 + 0 + {C0B} / {CLB} / L + {CL} fL) / dt = - {Q2} fo ~ {6 c} / L >
在103年或更短的时间尺度上代表碳守恒定律。
类似地,式(2.7.1)-式(2.7.5)在经度上的积分及其结果相加得到
2 na因为< p S ((CA) + (C0) / o +(棒子)/ o + (Clb) / L + [QJ / D / df
+ 8(MCTa + MCT0 + MCTL)/a d
m0(v0c0 - i - vQcOB)a cos cp dX,其中
它是mAvAcAa cos < pdx o
2n mLvLcLa cos (p dX, o)为海洋、大气和岩石圈的经向碳运移。
如果我们翻到(2.7.7),假设([ô£]/o + LQhlfi) = 0> MCFL = 0,可以得到MCTA和MCT0的粗略估计。考虑到大气和海洋的经向碳输运必须在极点消失,我们得到,年平均(MCTA 4- MCT0) = 0,即大气和海洋的年平均经向碳输运必须相互平衡。那么,让我们回想一下,海洋在低纬度地区是大气的碳源,在高纬度地区是大气的碳吸收器,在赤道地区,海洋和大气之间的年平均碳交换强度就说明了这一点
GtC ~ 0.8 /年。因此,年平均经向碳输运在大气中是从低纬度向高纬度的,而在海洋中则相反。此外,由于大气和海洋的质量和纬向扩展的比值分别等于3 × 10英寸3和2,那么,在所有条件相同的情况下,大气中跨纬度圈单位长度的经向碳运输的典型值必须比海洋中大两个数量级。为了将相对单位转换为绝对单位,我们注意到,在前工业时代,当大气中二氧化碳的源和汇平均每年相互平衡时,大气中二氧化碳的经向输送为3-6 GtC/年。
小尺度海洋-大气相互作用
3.1地面大气层
表面大气层在其范围内动量、热量和水分的垂直通量保持高度近似恒定的一层。让我们扩展一下这个定义。
我们检查平均(在雷诺条件下)运动方程的水平速度矢量v.与统计齐次(在水平方向上)速度场,它采取的形式,其中p是大气压力;X为切向风应力的水平矢量;P是空气密度;d/dt和V是总导数和水平梯度的算子;z轴垂直向上;K是沿z轴方向的单位向量。
式(3.1.1)右边的前两项分别表示科里奥利力和水平压力梯度力的作用,是主要的项。考虑到二者相互平衡,则假设fu0(其中u0为特征风速尺度;/是(3.1.1)右侧第三项的上估计,向量x/p在垂直方向上的变化为0.2|t|/p,我们得到垂直动量通量近似恒定的层厚h1的不等式:hl >0.2 (|t|/p)(/m0)_1,由\x\/p = 0.1 m2/s2, u0 = 10m/s, / = 10"4 s-1,得到hx > 20 m的估计。
垂直热通量H近似恒定的层的厚度h2可以从平均热平衡方程中得到,在没有水蒸气跃迁的情况下,平均热平衡方程和辐射源以及p dz p dv di p dz p
下沉的热量,被写成
继续阅读:电阻定律和热湿交换定律
这篇文章有用吗?

